参考答案：[证明] (1)A²=(E-ξξ^T)(E-ξξ^T)=E-2ξξ^T+ξξ^Tξξ^T
=E-ξξ^T+ξ(ξ^Tξ)ξ^T-ξξ^T=A+(ξ^Tξ)ξξ^T-ξξ^T
那么A²=A

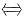(ξ^Tξ-1)ξξ^T=0．
因为ξ是非零列向量，ξξ^T≠0，故A²=A

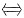ξ^Tξ-1=0．即ξ^Tξ=1．
(2)反证法．当ξ^Tξ=1时，由(1)知A²=A，若A可逆，则
A=A^-1A²=A^-1A=E
与已知A=E-ξξ^T≠E矛盾．