问题
单项选择题
设A是任一n(n≥3)阶方阵,A*是其伴随矩阵,又k为常数,且k≠0,±1,则必有(kA)*=______
(A) kA*. (B) kn-1A*. (C) knA*. (D) k-1A*.
答案
参考答案:B
解析: 对任何n阶矩阵都要成立的关系式,对特殊的n阶矩阵自然也要成立.那么,当A可逆时,由A*=|A|A-1有
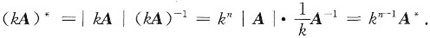
故应选(B).
一般地,若A=(aij),有kA=(kaij),那么矩阵kA的i行j列元素的代数余子式为
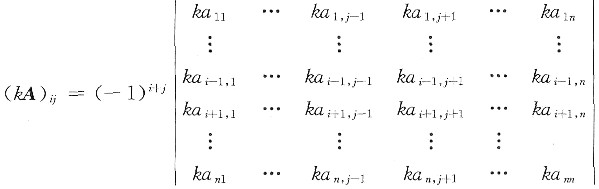
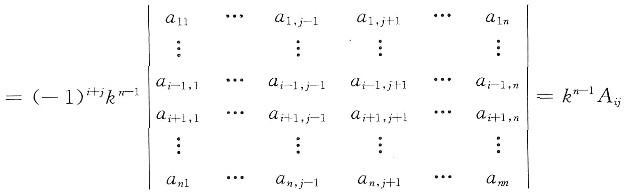
即|kA|中每个元素的代数余子式恰好是|A|相应元素的代数余子式的kn-1倍,因而,按伴随矩阵的定义知(kA)*的元素是A*对应元素的kn-1倍.
