问题
解答题
设函数f（x）=x2+|x-2|-1，x∈R，
（Ⅰ）判断函数f（x）的奇偶性；
（Ⅱ）求函数f（x）的最小值。
答案
解：（Ⅰ）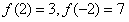
，
由于
，
故f（x）既不是奇函数，也不是偶函数。
（Ⅱ）
，
由于f（x）在[2，+∞)上的最小值为f（2）=3，在(-∞，2)内的最小值为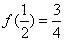
，
故函数f（x）在(-∞，+∞)内的最小值为
。
搜题请搜索小程序“爱下问搜题”
设函数f（x）=x2+|x-2|-1，x∈R，
（Ⅰ）判断函数f（x）的奇偶性；
（Ⅱ）求函数f（x）的最小值。
解：（Ⅰ），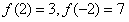
由于，
故f（x）既不是奇函数，也不是偶函数。
（Ⅱ），
由于f（x）在[2，+∞)上的最小值为f（2）=3，在(-∞，2)内的最小值为，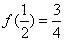
故函数f（x）在(-∞，+∞)内的最小值为。