问题
问答题
某高速公路边的交通警示牌有如图1所示的标记,其意义是指车辆的瞬时速度不得超过90km/h.若车辆驾驶员看到前车刹车后也相应刹车,反应时间是1s,假设车辆刹车的加速度相同,安全距离是两车不相碰所必须保持的距离的2倍,则车辆行驶在这条公路上的安全距离为多大?
甲同学这样车速v0=
=25m/s,末速vt=0.90 3.6
作v-t图求解.从图2中可得两车所要保持的距离就是平行四边形abcd的面积,其面积恰等于矩形Oace的面积,即:Sabcd=25×1=25m,所以安全距离为50m.
而乙同学认为甲同学的分析不够全面,只分析了一种情况,乙同学认为安全距离应该大于50m.
你认为哪位同学的结果正确?为什么?请予以说明并有解答过程(也可在图3中作图并说明).

答案
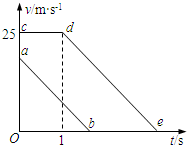
甲同学的结论不正确,因为他只考虑了前后两辆车都以90km/h即25m/s的速度行驶的情况,即:v前=v后,其实还存在这样两种情况:
(1)v前=25m/s,v后<25m/s;(2)v前<25m/s,v后=25m/s.
显然(1)中v前=25m/s,v后<25m/s的情况下安全距离小于50m.
而(2)中v前<25m/s,v后=25m/s的情况下安全距离要大于50m,可从v-t图中可知:两车不相碰距离就是面积Scabed>25m,所以安全距离要大于50m.
答:乙同学分析分析正确,甲同学的结论不正确,因为他只考虑了前后两辆车都以90km/h即25m/s的速度行驶的情况.
