问题
解答题
设函数f（x）=x3+bx2+cx（x∈R），已知g（x）=f（x）-f′（x）是奇函数。
（Ⅰ）求b、c的值；
（Ⅱ）求g（x）的单调区间与极值。
答案
解：（Ⅰ）∵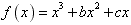
，
∴
，
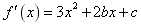从而
是一个奇函数，所以
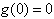得c=0，
由奇函数定义得b=3；
（Ⅱ）由（Ⅰ）知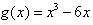
，从而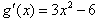
，
由此可知，
是函数g（x）是单调递增区间；
是函数g（x）是单调递减区间；
∴g（x）在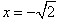
时，取得极大值，极大值为
；
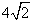g（x）在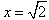
时，取得极小值，极小值为
。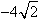