问题
解答题
已知抛物线 y=x2﹣4与直线y=x+2．
（1）求两曲线的交点；
（2）求抛物线在交点处的切线方程．
答案
解：（1）由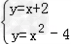
，
求得交点A（﹣2，0），B（3，5）
（2）因为y'=2x，则y'|x=﹣2=﹣4，y'|x=3=6，
所以抛物线在A，B处的切线方程分别为
y=﹣4（x+2）与 y﹣5=6（x﹣3）4x+y+8=0 与6x﹣y﹣13=0
搜题请搜索小程序“爱下问搜题”
已知抛物线 y=x2﹣4与直线y=x+2．
（1）求两曲线的交点；
（2）求抛物线在交点处的切线方程．
解：（1）由，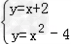
求得交点A（﹣2，0），B（3，5）
（2）因为y'=2x，则y'|x=﹣2=﹣4，y'|x=3=6，
所以抛物线在A，B处的切线方程分别为
y=﹣4（x+2）与 y﹣5=6（x﹣3）4x+y+8=0 与6x﹣y﹣13=0