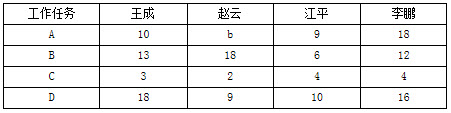
参考答案：

(1) 建立矩阵。 (2) 进行约减 (3) 画盖0线。 (4) 求最优解。 根据求得结果找到表2-2中对应的数据，即得如下结果： 王成完成C任务；赵云完成A任务；江平完成B任务；李鹏完成D任务。 完成任务的总时间=(2+5+6+9)小时=22小时。 计算步骤如下：

1) 建立矩阵

2) 对以上矩阵进行约减，即每一行数据减去本行的最小数，得出新矩阵为：

矩阵中第一列和第四列都不含“0”，因此转入第三步，进行列约减。

3) 对以上矩阵进行列约减，即每一列约减去本行数据中的最小数，得出新矩阵为：

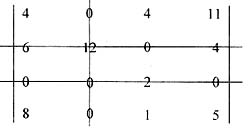
4) 在上述矩阵中画“盖0”线。即i画出最少的线将矩阵中的“0”全部覆盖住。“盖0”线只有2条，小于4，因此转入第五步进行数据转换。

5) 数据转换。上述矩阵中未被“盖0”线覆盖的最小数为1，将矩阵中未被“盖0”线覆盖的数减去1，“盖0”较差点处的数加1，得出新矩阵为：

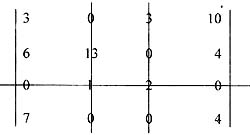
6) 在双数矩阵中画“盖0”线，“盖0”线只有1条小于矩阵的维数4，因此转入第七步，进行数据转换。

7) 数据转换。上述矩阵中未被“盖0”线覆盖的最小数为3，将矩阵中未被“盖0”线覆盖的数减3，“盖0”线交叉点处的数加3，得出新矩阵为：

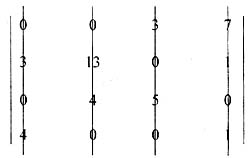
8) 在上述矩阵中画“盖0”线，“盖0”线有4条，等于矩阵的位数4，因此转入第九步，求得优解。 9) 求最优解。 ①最后一列只含有一个“0”，将该列中的“0”打“√”。 ②将第三列中另外一个“0”打“×”。 ③将第一列中另外一个“0”打“√”。 ④将第一行中另外一个“0”打“×”。 ⑤将第二列中另外一个“0”打“√”。 ⑥将第四行中另外一个“0”打“×”。 ⑦将第三列中另外一个“0”打“√”。 最终结果见下矩阵。

参照表2-2，最短时间为(3+2+4+4=13/4)小时=3．25小时。