问题
解答题
在等差数列{an}和等比数列{bn}中，a1=b1=1，b4=8，{an}的前10项和S10=55．
（Ⅰ）求an和bn；
（Ⅱ）已知cn=an+bn求cn的前n项之和Tn．
答案
（Ⅰ）设等差数列的公差为d，等比数列的公比为q．
∵a1=b1=1，b4=8，{an}的前10项和S10=55．
∴S10=10+
d=55；b4=q3=8；10×9 2
解得：d=1，q=2．
所以：an=n，bn=2n-1．
（Ⅱ）∵an=n，bn=2n-1，∴cn=an+bn=n+2n-1，
∴{cn}前n项之和Tn=（1+2+3+…+n）+（1+2+4+…+2n-1）
=
+n(n+1) 2 1-2n 1-2
=
+2n-1．n(n+1) 2
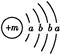,X的阳离子与Y的阴离子的电子层结构相同。元素Z、W均为短周期元素,它们原子的最外层电子数均是其电子层数的2倍,Z与Y相邻且Z、W能形成一种WZ2型分子。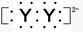
2Y-+Z↓