问题
解答题
求双曲线9x2-y2=81 的实轴长、虚轴长、顶点坐标、焦点坐标、渐近线方程、离心率．
答案
解：将9x2-y2=81 化为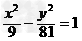
，
所以双曲线的焦点在x轴上，且a2=9，b2= 81．
从而a=3，b=9，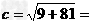
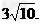
所以实轴长2a =6，虚轴长2b=18，
顶点坐标为(3，0)，（-3，0），焦点坐标为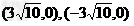
，渐近线方程为y=±3x，离心率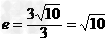
搜题请搜索小程序“爱下问搜题”
求双曲线9x2-y2=81 的实轴长、虚轴长、顶点坐标、焦点坐标、渐近线方程、离心率．
解：将9x2-y2=81 化为，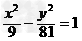
所以双曲线的焦点在x轴上，且a2=9，b2= 81．
从而a=3，b=9，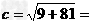
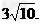
所以实轴长2a =6，虚轴长2b=18，
顶点坐标为(3，0)，（-3，0），焦点坐标为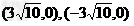，渐近线方程为y=±3x，离心率