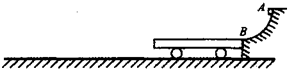
如图所示,AB为半径R=0.8m的
光滑圆孤轨道,下端B恰与小车右墙平滑对接.小车的质量m=3kg、长度L=2.16m,其上表面距地面的髙度h=0.2m.现有 质量m=1kg的小滑块,由轨道顶端无初速度释放,滑到B端后冲上小车,当小车与滑块 达到共同速度时,小车被地面装置锁定.已知地面光滑,滑块与小车上表面间的动摩擦 因数u=0.3,取g=10m/s2o试求:1 4
(1)搰块经过B端时,轨道对它支持力的大小
(2)小车被锁定时,其右端到轨道B端的距离.
(3)小车被锁定后,滑块继续沿小车上表面滑动.请判断:滑块能否从小车的左端滑出小 车?若不能,请计算小车被锁定后由于摩擦而产生的内能是多少?若能,请计算滑块的 落地点离小车左端的水平距离.
(1)设滑块经过B点的速度为v1,由机械能守恒定律得:
mgR=1 2 mv 21
解得:v1=4m/s
设滑块经过B点时,轨道对其支持力为N,由牛顿第二定律得:
N-mg=mv 21 R
解得:N=30N
(2)当滑块滑上小车后,设滑块和小车加速度分别为a1、a2,由牛顿第二定律得:
对滑块:-μmg=ma1
对小车:μmg=Ma2
解得:a1=-3m/s2,a2=1m/s2
设经时间t1达到共同速度,其速度为v,由运动学公式得:
v=v1+a1t1
v=a2t1
解得:t1=1s,v=1m/s
设此时小车右端到B的距离为x1,由运动学公式得:
x1=1 2
=0.5ma2t 21
(3)设达到共同速度时,滑块的位移为x2,由运动学公式得:
x2=v1t1+1 2 a1t 21
解得:x2=2.5m
此时,滑块在小车表面滑动距离为△x1,则:
△x1=x2-x1=2.5-0.5m=2m
小车被锁定后,假设滑块能从另一端滑下,滑块又在小车表面滑动距离为△x2,由几何关系得:
△x2=L-△x1=0.16m
设滑块滑下时的速度为v2,由动能定理得:
-μmg△x2=1 2
-mv 22
mv21 2
解得:1 2
=0.02J>0mv 22
所以滑块能从左端滑出,且滑出的速度为v2=0.2m/s
滑块滑出后,做平抛运动,设落地时间为t2,落点到小车左端距离为x3,则:
h=1 2 gt 22
x3=v2t2
联立解得x3=0.04m
答:(1)搰块经过B端时,轨道对它支持力的大小为30N
(2)小车被锁定时,其右端到轨道B端的距离为0.5m
(3)滑块能从小车的左端滑出,落地点离小车左端的水平距离为0.04m
