如图所示，由双曲线的方程可知：a=1．

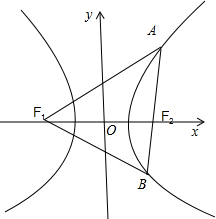
∴|AF₁|-|AF₂|=2，

∵|AF₂|=2，∴|AF₁|=4．

∴|F1F2|2=（2c）²=4²+2²-2×4×2×cos45°，化为c2=5-2

2

，

∴b2=c2-1=4-2

2

，

设A（x₁，y₁），B（x₂，y₂）．

则

(x1-c)2+ y 21 =2 b2 x 21 - y 21 =b2

，化为c2

x

21

-2cx1-3=0．

解得x1=

3

c

，x1=-

1

c

（舍去）．

由此解出A的坐标为（

3

c

，

4-( 3 c -c)2

），

设直线AB方程为x=my+c，与双曲线x2-

y2

b2

=1联解，可得(m2-

1

b2

)y2+2cmy+b2=0

由根与系数的关系，得到

y1+y2= 2cm 1 b2 -m2 y 1y2= b2 m2- 1 b2

，结合y₁=

4-( 3 c -c)2

化简得到|y₂|=（

2

-1）y₁

∴

S△BF1F2

S△AF1F2

=|

y2

y1

|=

2

-1

∵双曲线中，△AF₁F₂的面积S △AF 1F2=

b2

tan22.5°

=

4-2 2

2 -1

=2

2

∴△BF₁F₂的面积S △BF 1F2=（

2

-1）S △AF 1F2=4-2

2

由此可得△F₁AB及的面积S=S △AF 1F2+S △BF 1F2=4

故答案为：4