问题
填空题
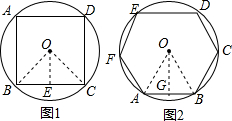
一个正方形和一个正六边形的外接圆半径相等,则此正方形与正六边形的面积之比为______.
答案
设圆的半径为R,
如图1,
连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=
R,2 2
故BC=
R;2
如图2,
连接OA、OB,过O作OG⊥AB,
则△OAB是等边三角形,
故AG=OA•cos60°=
R,AB=2AG=R,1 2
∴OG=
R,3 2
∴此正方形的面积为:
R×2
R=2R2,2
正六边形的面积为:6×
×R×1 2
R=3 2
R2,3 3 2
∴此正方形与正六边形的面积之比为:2R2:
R2=43 3 2
:9.3
故答案为:4
:9.3