问题
填空题
已知圆内接正方形的边长为
|
答案
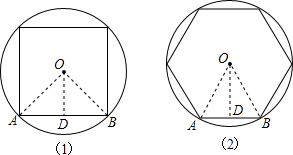
如图(1)所示,过O作OD⊥AB于D,连接OA,OB;
∵四边形是圆内接四边形,
∴∠AOB=
=90°;360° 4
∵OA=OB,OD⊥AB,
∴∠AOD=
=45°,90° 2
∴OD=AD=
AB=1 2
,2 2
OA=
=OD2+AD2
=1.(
)2+(2 2
)22 2
如图(2)所示,连接OA,OB,过O作OD⊥AB于D;
∵四边形是圆内接四边形,
∴∠AOB=
=60°,360° 6
∵OA=OB,
∴△AOB是正三角形,
∴OA=OB=AB=1.
即该圆的内接正六边形的边长为1.
故答案为:1.