问题
解答题
设等差数列{an}的前n项和为Sn,已知a3=24,S11=10.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)当n为何值时,Sn最大,并求Sn的最大值.
答案
(Ⅰ)设等差数列{an}的公差为d,依题意有
,a1+2d=24 11a1+
d=1011×10 2
解得
,a1=40 d=-8
∴数列{an}的通项公式为:an=40-8(n-1)=48-8n.
(Ⅱ)由(Ⅰ)知,∴an=48-8n,a1=40,
故Sn=
=n(a1+an) 2
=-4n2+44nn(40+48-8n) 2
(Ⅲ)由(Ⅱ)有,Sn=-4n2+44n=-4(n-
)2+12111 2
故当n=5或n=6时,Sn最大,且Sn的最大值为S5=S6=120.

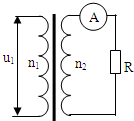
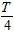 时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )
时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )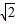
 :3
:3