问题
解答题
已知双曲线方程为2x2-y2=2 ．
(1) 过定点P(2 ，1) 作直线交双曲线于P1，P2两点，当点P(2 ，1) 是弦P1P2 的中点时，求此直线方程．
(2) 过定点Q(1 ，1) 能否作直线l ，使l 与此双曲线相交于Q1，Q2两点，且Q 是弦Q1Q2的中点？若存在，求出直线l的方程；若不存在，请说明理由.
答案
解：设y=kx-2k+1．
由
消y并化简，得（2-k2）x2+2k（2k-1）x-4k2+4k-3=0．
设直线与双曲线的交点P1（x1，y1），P2（x2，y2）．
当2-k2≠0即k2≠2时，
有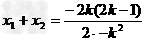
又点P(2，1)是弦P1P2的中点，
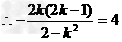，解得k=4．
当 k=4时
Δ=4k2 (2k-1)2-4(2-k2) (-4k2+4k-3)=56×5>0,
当k2=2即
时，
与渐近线的斜率相等，
即
的直线l与双曲线不可能有两个交点，
综上所述，所求直线方程为y=4x-7．
(2)假设这样的直线l存在，设Q1（x1，y1），Q2（x2，y2），
则有
∴x1+x2=2，y1+y2=2，
且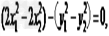
两式相减，得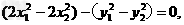
∴2(x1-x2)(x1+x2)-(y1-y2) (y1+y2)=0,
∴2(x1-x2)-（y1-y2)=0.
若直线Q1Q2⊥QX，则线段Q1Q2的中点不可能是点Q(1，1)，
所以直线Q1Q2有斜率，于是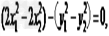
∴直线Q1Q2的方程为y-1=2（x-1），即y=2x-1．
由
得2x2-（2x-1）2=2， 即2x2-4x+3 =0，
∴Δ=16-24 <0．
这就是说，直线l与双曲线没有公共点，因此这样的直线不存在．