问题
填空题
设A是三阶矩阵，|A-E|=0，(2A-E)x=0有非零解，3A+E是不可逆矩阵，则
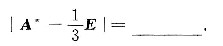
答案
参考答案：[*]
解析：方法一 因|A-E|=0，(2A-E)X=0有非零解，3A+E不可逆，故均有|A-E|=0，|2A-E|=0，|3A+E|=0，从而知三阶矩阵A有特征值
[*]
[*]
搜题请搜索小程序“爱下问搜题”
设A是三阶矩阵，|A-E|=0，(2A-E)x=0有非零解，3A+E是不可逆矩阵，则
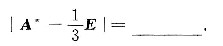
参考答案：[*]
解析：方法一 因|A-E|=0，(2A-E)X=0有非零解，3A+E不可逆，故均有|A-E|=0，|2A-E|=0，|3A+E|=0，从而知三阶矩阵A有特征值
[*]
[*]