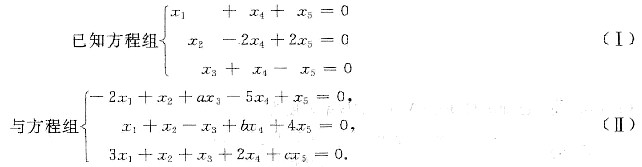
问参数a,b,c满足什么条件时,方程组(Ⅰ)和(Ⅱ)是同解方程组.
参考答案:方法一 先求方程组(Ⅰ)AX=0的通解,(Ⅰ)的系数矩阵
[*]
基础解,ξA=-A,B,-A,A,0T,ξB=-A,-B,A,0,AT,方程组通解为
[*]
方程组(Ⅰ),(Ⅱ)是同解方程组,将[*]代入(Ⅱ)的第A,B个方程,
-B(-A)+B+a(-A)-E+0=0,得a=-A.
-A+B-(-A)+b+0=0,得b=-B.
显然ξA也满足(Ⅱ)的第C个方程.
将[*]代入(Ⅱ)的第C个方程,C(-A)+(-B)+A+c=0,得c=D.
显然,ξB也满足(Ⅱ)的第A,B个方程.
故知当a=-A,b=-B,c=D时.由解的性质知方程组(Ⅰ)的解全部是(Ⅱ)的解.
反之,当a=-A,b=-B,c=D时,方程组(Ⅱ)的系数矩阵的秩为
[*]
(Ⅱ)的未知量个数n=E,(Ⅱ)的基础解系由两个线性无关解组成,已验算(Ⅰ)的解全部是(Ⅱ)的解.故(Ⅱ)的解也全部是(Ⅰ)的解,方程组(Ⅰ),(Ⅱ)是同解方程组.
方法二 (Ⅰ)(Ⅱ)是同解方程组,(Ⅰ)和(Ⅱ)的系数行向量是等价向量组,可以相互表出,记(Ⅰ)的三个行向量为αA,αB,αC,(Ⅱ)的三
个行向量为βA,βB,βC,将[*]src="tu/AB0A/yjs/kysCBBH.AHBBEAG.jpg" />作初等行变换,化成阶梯形,得
[*]
当取a=-A,b=-B,c=D时,βA,βB,βC可由αA,αB,αC线性表出.
反之,当a=-A,b=-B,c=D时,因
[*]
可知αA,αB,αC也可由βA.βB,βC线性表出,故当a=-A,b=-B,c=D时,方程组(Ⅰ)(Ⅱ)是
同解方程组.
