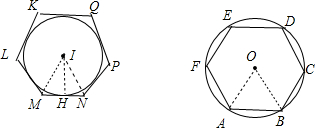
如图，设⊙I的半径为2x，⊙O的半径为3x，

作IH⊥MN于H，连结IM、IN、OA、OB，

∴MH=NH，

∵∠MIN=60°，

∴∠MIH=30°，

∴MH=

3

3

IH=

2 3

3

x，

∴MN=

4 3

3

x，

∴正六边形MNPQKL的面积=6•

1

2

•

4 3

3

x•2x=8

3

x²，

∵∠AOB=60°，

∴S_△OAB=

3

4

•（3x）²=

9 3

4

x²，

∴正六边形ABCDEF的面积=6•

9 3

4

x²=

27 3

2

x²，

∴正六边形MNPQKL的面积：正六边形ABCDEF的面积=8

3

x²：

27 3

2

x²=16：27．

故选C．