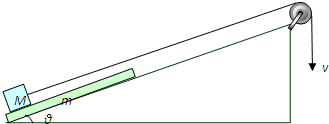
如图所示,斜面倾角为θ,一块质量为m、长为l的匀质板放在很长的斜面上,板的左端有一质量为M的物块,物块上连接一根很长的细绳,细绳跨过位于斜面顶端的光滑定滑轮并与斜面平行,开始时板的右端距离斜面顶端足够远.试求:
(1)若板与斜面间光滑,某人以恒力F竖直向下拉绳,使物块沿板面由静止上滑过程中,板静止不动,求物块与板间动摩擦因数μ0;
(2)在(1)情形下,求物块在板上滑行所经历的时间t0;
(3)若板与物块和斜面间均有摩擦,且M=m,某人以恒定速度v=
,竖直向下拉绳,物块最终不滑离板的右端.试求板与物块间动摩擦因数μ1和板与斜面间动摩擦因数μ2必须满足的关系.2glsinθ
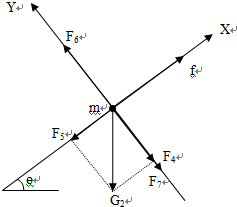
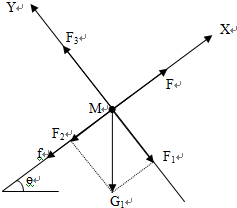
(1)分别对物块和木板受力分析并建立如图所示的直角坐标系,
对木块M:G1=Mg,则:F1=Mgcosθ,
又:M在Y轴方向受力平衡,
所以F3=F1=Mgcosθ.
又:f=μ0F1=μ0Mgcosθ
对板m:因为静止,所以X、Y方向分别受力平衡:
X轴方向:F5=G2sinθ=mgsinθ;f=μ0Mgcosθ;
所以:mgsinθ=μ0Mgcosθ;
得:μ0=
•tanθm M
(2)设物块M的加速度为a0,物块Y方向合力为零,所以合力即为X轴上的合力:
X轴方向:F2=G1sinθ=Mgsinθ;f=μ0Mgcosθ;
所以:F合=F-Mgsinθ-μ0Mgcosθ
由牛顿第二定律:F=ma得:
F-Mgsinθ-μ0Mgcosθ=Ma0
即:a0=F-Mgsinθ-μ0Mgcosθ M
又:l=
a01 2
带入数据得:t 20
联立解得:t0=2Ml F-(M+m)gsinθ
(3)设物块在板上滑行的时间为t1,板的加速度为a,
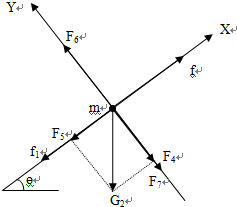
对板有:Y方向合力为零,所以合力即为X方向的合力:
X轴方向:f=μ1Mgcosθ;f1=μ2(M+m)gcosθ;F5=G2sinθ=mgsinθ
所以:F合=μ1Mgcosθ-mgsinθ-μ2(M+m)gcosθ
由牛顿第二定律:F=ma得:
μ1Mgcosθ-mgsinθ-μ2(M+m)gcosθ=ma①
且物块最终不滑离板的右端.说明物块和木板最终要达到相同的速度v:所以有:v=at1②
①②联立解得 t1=mv μ1Mgcosθ-mgsinθ-μ2(M+m)gcosθ
又设物块从板的左端运动到右端的时间为t2,
则:vt2-
vt2=l1 2
t2=2l v
为使物块最终不滑离板的右端,必须满足 t1≤t2
即
≤mv μ1Mgcosθ-mgsinθ-μ2(M+m)gcosθ 2l v
代入v=
解得:μ1-2μ2≥2tanθ2glsinθ
所以要使物块最终不滑离板的右端,μ1与μ2必须满足μ1-2μ2≥2tanθ
答:
(1)物块与板间动摩擦因数μ0=
•tanθ.m M
(2)在(1)情形下,求物块在板上滑行所经历的时间t0=2Ml F-(M+m)gsinθ
(3)若板与物块和斜面间均有摩擦,且M=m,某人以恒定速度v=
,竖直向下拉绳,物块最终不滑离板的右端.试求板与物块间动摩擦因数μ1和板与斜面间动摩擦因数μ2必须满足的关系为:μ1-2μ2≥2tanθ2glsinθ

 宇六合的恐怖一样的死寂包裹着,听着马蹄声单调地试探着和这静默碰击,不由得屏住了呼吸。
宇六合的恐怖一样的死寂包裹着,听着马蹄声单调地试探着和这静默碰击,不由得屏住了呼吸。 谨慎地选择着落蹄之地,我在曝晒中晕眩了,怔怔地觉得马的脚踝早已被那些尖利的石刃割破了。
谨慎地选择着落蹄之地,我在曝晒中晕眩了,怔怔地觉得马的脚踝早已被那些尖利的石刃割破了。 三条巨流般的黑戈壁,寸草不生,平平地铺向三个可怕的远方。因此,地图上又标着另一个地名叫三岔口;这个地点在以后我的生涯中总是被我反复回忆,咀嚼吟味,我总是无法忘记它。仿佛它是我人生的答案。
三条巨流般的黑戈壁,寸草不生,平平地铺向三个可怕的远方。因此,地图上又标着另一个地名叫三岔口;这个地点在以后我的生涯中总是被我反复回忆,咀嚼吟味,我总是无法忘记它。仿佛它是我人生的答案。 枚被人丢弃的棋子,如一粒生锈的弹丸,孤零零地存在于这巨大得恐怖的大自然中。
枚被人丢弃的棋子,如一粒生锈的弹丸,孤零零地存在于这巨大得恐怖的大自然中。