问题
单项选择题
设f(x)为R上不恒等于零的奇函数,且f’(0)存在,则函数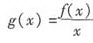 ()。
()。
A.在x=0处左极限不存在
B.有跳跃间断点x=0
C.在x=0处右极限不存在
D.有可去间断点x=0
答案
参考答案:D
解析:
[考点] 极限、间断点
由题设,f(-x)=-f(x),则有f(0)=0,
从而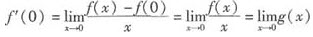 ,
,
即g(x)在x=0处极限存在,但x=0时g(x)无定义,
因此可补充定义g(0)=f’(0),则g(x)在x=0处连续.
综上,g(x)有可去间断点x=0,所以选(D).
