问题
填空题
设矩阵A,B满足A*BA=2BA-8E,其中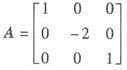 ,E为单位矩阵,A*为A的伴随矩阵,则B=()。
,E为单位矩阵,A*为A的伴随矩阵,则B=()。
答案
参考答案:

解析:
[考点] 矩阵方程
由已知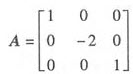 ,则|A|=-2≠0,
,则|A|=-2≠0,
由公式AA*=A*A=|A|E化简矩阵方程A*BA=2BA-8E,
即分别以A左乘该方程,以A-1右乘该方程得-2B=2AB-8E,
从而2(A+E)B=8E.即(A+E)B=4E,因此B=4(A+E)-1,
其中
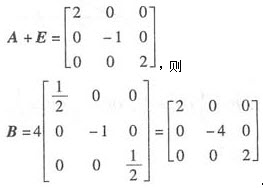
设矩阵A,B满足A*BA=2BA-8E,其中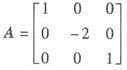 ,E为单位矩阵,A*为A的伴随矩阵,则B=()。
,E为单位矩阵,A*为A的伴随矩阵,则B=()。
参考答案:

解析:
[考点] 矩阵方程
由已知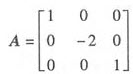 ,则|A|=-2≠0,
,则|A|=-2≠0,
由公式AA*=A*A=|A|E化简矩阵方程A*BA=2BA-8E,
即分别以A左乘该方程,以A-1右乘该方程得-2B=2AB-8E,
从而2(A+E)B=8E.即(A+E)B=4E,因此B=4(A+E)-1,
其中