问题
单项选择题
设f(x,y)与φ(x,y)均为可微函数,且φ’y(x,y)≠0,已知(x0,y0)是f(x,y)在约束条件φ(x,y)=0下的一个极值点,下列选项正确的是()。
A.若f’x(x0,y0)=0,则f’y(x0,y0)=0
B.若f’x(x0,y0)=0,则f’y(x0,y0)≠0
C.若f’x(x0,y0)≠0,则f’y(x0,y0)=0
D.若f’x(x0,y0)≠0,则f’y(x0,y0)≠0
答案
参考答案:D
解析:
[考点] 二元函数条件极值问题
依题意知(x0,y0)是拉格朗日函数,F(x,y,λ)=f(x,y)+λφ(x,y)的驻点,即(x0,y0)使得
因为φ’y(x0,y0)≠0,所以从(2)式可得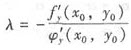 ,
,
代入(1)式得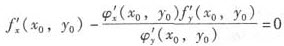 ,
,
即f’x(x0,y0)φ’y(x0,y0)=φ’x(x0,y0)f’y(x0,y0).
当f’x(x0,y0)≠0且φ’y(x0,y0)≠0时,f’x(x0,y0)φ’y(x0,y0)≠0,
从而f’y(x0,y0)≠0,故选(D).
