问题
问答题
设三阶实对称矩阵A的各行元素之和均为3,向量α1=(-1,2,-1)T,α2=(0,-1,1)T是线性方程组Ax=0的两个解.
求A的特征值与特征向量。
答案
参考答案:
依题意,因为
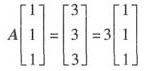
所以3是矩阵A的一个特征值,α=(1,1,1)T是A属于3的特征向量,
又因为Aα1=0=0α1,Aα2=0=0α2,所以α1,α2是矩阵A属于λ=0的特征向量,所以A的特征值是3、0、0,且λ=0的特征向量为
k1(-1,2,-1)T+k2(0,-1,1)T(k1,k2是不全为0的常数),λ=3的特征向量为k=(1,1,1)T(k≠0为常数).
