问题
单项选择题
设Am×n=(α1，α2…，αn)=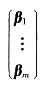
(m＞n)下述判断正确的是（）。
A．因m＞n，所以r(β1，…，βm)＞r(α1，α2…，αn)
B．若r(A)=n，则方程组AX=0没有非零解
C．若α1，α2…，αn线性无关，则β1，…，βm也无关
D．若r(A)=r＜n，则α1，α2…，αn中任意r个向量线性无关
答案
参考答案：B
解析：
A矩阵只不过是改变了形式，行秩=列秩，即错误。
B若r(A)=n，方程组有唯一解，对于AX=0齐次线性方程组，唯一解必为零解，因此B正确。
Cβ1，β2，…βm个数为m，βi的维数为n，m＞n，即个数大于维数，β1，β2，…βm必相关，α1，α2，…αn无关也没用，C错误。
D若α1，α2，…αn中含有αi=0的向量，则任意r个向量中有相关的，因此D错误。选B。