问题
单项选择题
3阶矩阵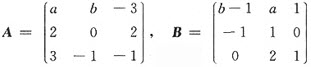 。知r(AB)小于r(A)和(B),a+b+r(AB)=()。
。知r(AB)小于r(A)和(B),a+b+r(AB)=()。
A.4
B.5
C.6
D.7
答案
参考答案:A
解析:
此题关键考查r(AB)<min[r(A),r(B)]
(1)首先根据性质,当A可逆时,r(AB)=r(B)。
(2)A可逆,即A为满秩r(A)=3,在此题中,若r(A)=3,r(B)r3,则有r(AB)=r(B)=3,
这样就无法满足条件中的r(AB)<r(A),r(AB)<r(B)。
因此必须有r(A)≤2,r(B)≤2,这样隐含的意义就被挖出来了。

若要使得r(A)≤2,r(B)≤2,则有

此时r(A)=r(B)=2。若r(AB)<r(A)=r(B)=2,则r(AB)=1(可进一步计算出AB,再看它的秩,最终求出r(AB)=1)。故选A。
