问题
单项选择题
ζ1,ζ2,ζ3是AX=0的一个基础解系,α1,α2,α3也是AX=0的一个基础解系()。
A.α1=ζ1-ζ2,α2=ζ2-ζ3,α33=ζ3-ζ1
B.α1=ζ1+ζ2,α2=ζ2+ζ3,α33=ζ3+ζ1
C.α1=ζ1-ζ2,α2=2ζ2,α33=ζ2-ζ1
D.α1=2ζ1-ζ2-ζ3,α2=ζ2-ζ1,α33=ζ3-ζ1
答案
参考答案:B
解析:
B中(α1,α2,α3)=(β1,β2,β3)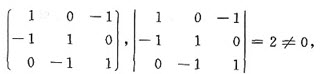
所以构成基础解系,选B。
