问题
单项选择题
已知a为实数，在实数范围对整式x8-a8分解因式，运算到x8-a8为若干个因式的乘积，每个因式不能再分解了，此时这个乘积共有（）。
A．2个一次因式，3个二次因式
B．4个一次因式，2个二次因式
C．2个一次因式，1个二次因式，1个四次因式
D．2个一次因式，2个三次因式
答案
参考答案：A
解析：
由分解因式的性质，在实数范围内最后分解为一次和二次因式，故可否定选项C、D。易见x8-a8=(x-a)(x+a)(x2+a2)(x4+a4)，不存在实数x使x2+a2=0或x4+a4=0，故x2+a2和x4+a4没有一次因式，后者可分懈为两个二次因式。故正确答案为A。
事实上，若在复数范围内分解，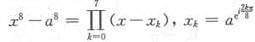
，k=0，1，…，7。
其中(x-x0)(x-x4)=(x-a)(x+a)
(x-x2)(x-x6)=(x-ai)(x+ai)=x2+a2
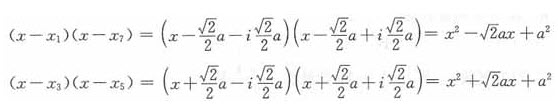
故正确答案为A。
