问题
问答题
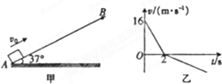
如图甲所示,有一足够长的粗糙斜面,倾角θ=37°,一滑块以初速度v0=16m/s从底端A点滑上斜面,滑至B点后又返回到A点.滑块运动的图象如图乙所示,
求:(已知:sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2)
(1)AB之间的距离.
(2)滑块再次回到A点时的速度.
(3)滑块在整个运动过程中所用的时间.
答案
(1)由图知 S=
m=16m 16×2 2
(2)滑块由A到B a1=
=△v △t
=8m/s2;16 2
上滑过程受重力、支持力和摩擦力,根据牛顿第二定律,有:
mgsinθ+μmgcosθ=ma1;
解得a1=g(sinθ+μcosθ) ①
由B到A过程,受重力、支持力和摩擦力,根据牛顿第二定律,有:
mgsinθ-μmgcosθ=ma2;
解得:a2=g(sinθ-μcosθ) ②
由以上各式得 a2=4m/s2;
vA=
=82a2S
m/s;2
(3)A到B过程,由图象得到:t1=2s;
B到A过程,由速度时间关系公式得到:t2=
=2vA a2
s2
t=t1+t2=2(1+
)s2
答:(1)AB之间的距离为16m;
(2)滑块再次回到A点时的速度为8
m/s;2
(3)滑块在整个运动过程中所用的时间为2(1+
)s.2
