问题
单项选择题
已知f(x)=x3-2x2+ax+b除以x2-x-2的余式为2x+1,则a、b的值是()。
A.a=1,b=-3
B.a=-3,b=1
C.a=-2,b=3
D.a=1,b=3
答案
参考答案:D
解析:
可直接由除法求解。

故余式=2x+1=(a+1)x+(b-2)
从而有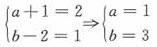
另解:设f(x)除以x2-x-2的商式为Q(x),则
x3-2x2+ax+b=(x2-x-2)Q(x)+2x+1
=(x-2)(x+1)Q(x)+2x+1
由余数定理 f(2)=2a+b=2×2+1=5
①
f(-1)=-3-a+b=2(-1)+1=-1
②
联立①和②,a、b的值可求得。
故正确答案为D。
