问题
单项选择题
要使方程3x2+(m-5)x+m2-m-2=0的两个实根分别满足0<x1<1和1<x2<2,实数m的取值范围是()。
A.-2<m<-1
B.-4<m<-1
C.-4<m<-2
D.-3<m<1
答案
参考答案:A
解析:
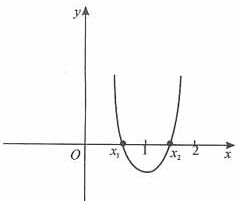
如图所示,设f(x)=3x2+(m-5)x+m2-m-2
则f(x)开口向上,与x轴交于(x1,0)和(x2,0)两点,有不等式组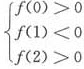 ,从而有
,从而有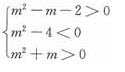
这里主要考查二次函数(方程)的性质。如果用一元二次方程根与系数的关系解题,比较繁琐,我们不妨结合图形解题。
