参考答案：

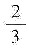
解析： 本题是求[*]型未定式的极限．从分子和分母的表达式不难发现，若直接利用洛必达法 则会碰到复杂的计算．为简化计算过程，应当在分子和分母中分别利用等价无穷小代换．
当x→0时，有 e^x-e^sinx=e^sinx(ex-^sinx-1)．
又因 e^x-sinx～x-sinx，[*]，于是，分子可用x-sinx代换．
当x→0时，[*]是无穷小量，于是分母可作等价无穷小代换，即
[*]
即得 [*]
[评注] 在本题的求解中用到了等价无穷小量的传递生质。若α，β，γ是同一极限过程的无穷小量，且α～β，β～γ，则α～γ，从而当x→0时
[*]