问题
填空题
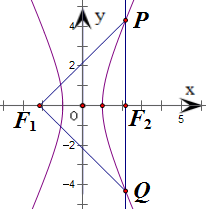
过双曲线的一个焦点F2作垂直于实轴的弦PQ,F1是另一焦点,若∠PF1Q=
|
答案
根据双曲线的对称性得|PF1|=|QF1|,
∵△PQF1中,∠PF1Q=
,π 2
∴△PQF1是等腰直角三角形,且被F1F2分成两个全等的等腰直角三角形
因此,Rt△PF1F2中,|F1F2|=|PF2|=2c,|PF1|=
|F1F2|=22
c2
∵|PF1|-|PF2|=2a,
∴2
c-2c=2a,可得a=(2
-1)c2
由此可得,双曲线的离心率e=
=c a
=c (
-1)c2
+12
故答案为:
+12
