问题
解答题
已知f(x)是R上的奇函数,且当x∈(﹣∞,0)时,f(x)=﹣xlg(2﹣x),求f(x)的解析式.
答案
解∵f(x)是奇函数,可得f(0)=﹣f(0),
∴f(0)=0.
当x>0时,﹣x<0,由已知f(﹣x)=xlg(2+x),
∴﹣f(x)=xlg(2+x),即f(x)=﹣xlg(2+x)(x>0).
∴f(x)= 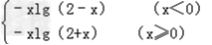
即f(x)=﹣xlg(2+|x|)(x∈R).
已知f(x)是R上的奇函数,且当x∈(﹣∞,0)时,f(x)=﹣xlg(2﹣x),求f(x)的解析式.
解∵f(x)是奇函数,可得f(0)=﹣f(0),
∴f(0)=0.
当x>0时,﹣x<0,由已知f(﹣x)=xlg(2+x),
∴﹣f(x)=xlg(2+x),即f(x)=﹣xlg(2+x)(x>0).
∴f(x)= 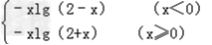
即f(x)=﹣xlg(2+|x|)(x∈R).