问题
解答题
设函数f(x)在(-∞,+∞)上满足f(2-x)=f(2+x),f(7-x)=f(7+x),且在闭区间[0,7]上,只有f(1)=f(3)=0,
(Ⅰ)试判断函数y=f(x)的奇偶性;
(Ⅱ)试求方程f(x)=0在闭区间[-2005,2005]上的根的个数,并证明你的结论。
答案
解:(Ⅰ)由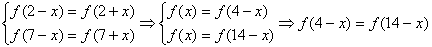
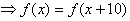 ,
,
又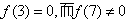 ,
,

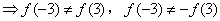 ,
,
故函数y=f(x)是非奇非偶函数;
(Ⅱ)由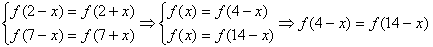
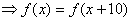 ,
,
又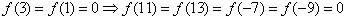 ,
,
故f(x)在[0,10]和[-10,0]上均有有两个解,
从而可知函数y=f(x)在[0,2005]上有402个解,在[-2005,0]上有400个解,
所以函数y=f(x)在[-2005,2005]上有802个解。
