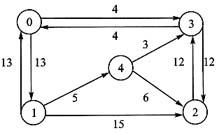
参考答案：[解答] 该图的邻接矩阵如下：

利用Floyd算法可求得两顶点之间最短路径长度。最后求得：

从A₄中可求得每对村庄之间的最少交通代价。假设医院建在i村庄时，其他各村庄
往返总的交通代价如下所示：
医院建在村庄0时，各村庄往返总的交通代价为12+16+4+7+13+16+4+18=90：
医院建在村庄1时，各村庄往返总的交通代价为13+29+17+20+12+11+8+5=115：
医院建在村庄2时，各村庄往返总的交通代价为16+11+12+6+16+29+12+34=136：
医院建在村庄3时，各村庄往返总的交通代价为4+8+12+3+4+17+12+22=82：
医院建在村庄4时，各村庄往返总的交通代价为18+5+34+22+7+20+6+3=115。
显然，把医院建在村庄3时总体交通代价最少。

解析： 本题主要考查Floyd算法的思想和解题步骤。Floyd算法的基本思想是：
假设求从顶点υ_i到υ_j的最短路径。如果从υ_i到υ_j有弧，则从υ_i到υ_j存在一条长度为arcs[i][j]的路径，该路径不一定是最短路径，尚需进行n次试探。
(1)首先考虑路径(υ_i，υ₀，υ_j)是否存在，即判别弧(υ_i，υ₀)和(υ₀,υ_j)是否存在。如果存在，则比较(υ_i，υ_j)和(υ_i,υ₀，υ_j)的路径长度，取长度较短者为从υ_i到υ_j的中间顶点的序号不大于0的最短路径。
(2)假如在路径上再增加一个顶点υ₁，也就是说，如果(υ_i，…，υ₁)和(υ₁，…，υ_j)分别是当前找到的中间顶点的序号不大于0的最短路径，那么(υ_i，…，υ₁，…，υ_j)就有可能是从υ_i到υ_j的中间顶点的序号不大于1的最短路径。将它和已经得到的从υ_i到υ_j中间顶点序号不大于0的最短路径相比较，从中选出中间顶点的序号不大于1的最短路径之后，再增加一个顶点υ₂，继续进行试探。依次类推。
(3)在一般情况下，若(υ_i，…，υ_k)和(υ_k，…，υ_j)分别是从υ_i到υ_k和从υ_k到υ_j的中间顶点的序号不大于k-1的最短路径，则将(υ_i，…，υ_k，…，υ_j)和已经得到的从υ_i到υ_j且中间顶点序号不大于k-1的最短路径相比较，其长度较短者便是从υ_i到υ_j的中间顶点的序号不大于k的最短路径。这样，在经过n次比较后，最后求得的必是从υ_i到υ_j的最短路径。
(4)按此方法，可以同时求得各对顶点间的最短路径。