某公司计划从国外引进电脑生产线，该项目分两期进行：第一期设备投资20000万元，于2008年初进行，建成后年产销量为1万台，销售单价1.2万元/台，单位变动成本0.6万元/台，每年固定付现经营成本为400万元，预计使用寿命为5年，预计能够收回的净残值率为原值的4%；第二期设备投资36000万元，于2010年初进行，建成后年产销量新增1.9万台，销售单价1.2万元/台，单位变动成本0.58万元/台，年固定付现经营成本新增760万元，预计使用寿命为5年，净残值率为原值的3%。
该公司两期投资均为当年投资当年完工投产，第二期项目的投资决策必须在2009年年底确定。该生产线税法规定的折旧方法为直线法，折旧年限为5年，用直线法提折旧，净残值率为原值的5%。生产电脑相比公司股票价格的方差为0.09，该公司要求的最低投资报酬率为15%(其中无风险报酬率为5%)；适用的所得税税率为25%。
要求：
(1)在不考虑期权的前提下，计算分析该项目第一期和第二期投资的可行性。
(2)在考虑期权的前提下，计算分析该项目第一期和第二期投资的可行性(第二期项目设备投资额按5%折现，其余按15%的折现率折现)。
参考答案：
(1)不考虑期权
①第一期：
年折旧＝
＝3800(万元)
年息税前利润＝(1.2-0.6)×10000-(400+3800)＝1800(万元)
年息前税后利润＝1800×(1-25%)＝1350(万元)
经营期第1～4年经营净现金流量＝息前税后利润+折旧＝1350+3800
＝5150(万元)
净残值损失抵税＝20000×(5%-4%)×25%＝50(万元)
经营期第5年经营净现金流量＝息前税后利润+折旧+净残值收入+净残值损失抵税
＝1350+3800+20000×4%+50
＝6000(万元)
净现值＝5150×(p/A，15%，4)+6000×(p/s，15%，5)-20000
＝5150×2.8550+6000×0.4972-20000
＝-2313.55(万元)
②第二期：
年折旧＝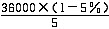
＝6840(万元)
年息税前利润＝(1.2-0.58)×19000-(760+6840)＝4180(万元)
年息前税后利润＝4180×(1-25%)＝3135(万元)
经营期第1～4年经营净现金流量＝息前税后利润+折旧＝3135+6840
＝9975(万元)
净残值损失抵税＝36000×(5%-3%)×25%＝180(万元)
经营期第5年经营净现金流量＝息前税后利润+折旧+净残值收入+净残值损失抵税
＝3135+6840+36000×3%+180
＝11235(万元)
净现值＝[9975×(p/A，15%，4)+11235×(p/s，15%，5)]×(p/s，15%，2)-36000×(p/s，5%，2)
＝(9975×2.8550+11235×0.4972)×0.7561-36000×0.9070
＝-6895.70(万元)
在不考虑期权的前提下，由于两期的净现值均小于0，所以均不可行。
(2)考虑期权
在考虑期权的前提下，可以将第二期投资看作是到期时间为2年的欧式看涨期权。
期权执行价格的现值＝36000×(p/s，5%，2)＝36000×0.9070
＝32652(万元)
预计未来经营现金流量＝[9975×(p/A，15%，4)+11235×(p/s，15%，5)]×(p/s，15%，2)
＝(9975×2.8550+11235×0.4972)×0.7561
＝34064.67(万元)
期权标的资产的当前价格＝34064.67×(p/s，5%，2)
＝34064.67×0.9070
＝25757.78(万元)
根据布莱克一斯科尔斯期权定价模型计算：
N(-0.3464)＝1-N(0.3464)＝1-0.6355＝0.3645
通过N(0.77)＝0.7794和N(0.78)＝0.7823之间插值来计算N(0.7707)：
N(0.7707)＝0.7794+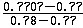
×(0.7823-0.7794)＝0.7796
N(-0.7707)＝1-N(0.7707)＝1-0.7796＝0.2204
C0＝S0N(d1)-pv(X)N(d2)
＝25757.78×0.3645-32652×0.2204
＝2192.21(万元)
由于第一期投资考虑期权后的净现值＝-2313.55+2192.21
＝-121.34(万元)
因此投资第一期和第二期项目均不可行。
