搜题请搜索小程序“爱下问搜题”
问题 填空题
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左焦点F（-c，0）（c＞0），作圆x2+y2=
a2
4
的切线，切点为E，延长FE交双曲线右支于点P，若
OE
=
1
2
(
OF
+
OP
)，则双曲线的离心率为______．
答案

∵

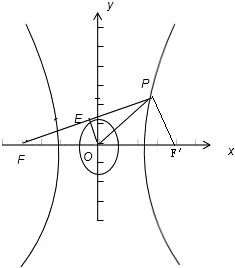
OE
=
1
2
(
OF
+
OP
)，

∴E为PF的中点，令右焦点为F′，则O为FF′的中点，

则PF′=2OE=a，

∵E为切点，

∴OE⊥PF

∴PF′⊥PF

∵PF-PF′=2a

∴PF=PF′+2a=3a

在Rt△PFF′中，PF2+PF′2=FF′2

即9a2+a2=4c2

⇒所以离心率e=

c
a
=
10
2

故答案为：

10
2
．

阅读理解与欣赏

阅读下面这首宋诗，回答问题。（8分）

吴松【注】道中二首（其二）

晁补之

晓路雨萧萧， 江乡叶正飘。

天寒雁声急， 岁晚客程遥。

鸟避征帆却， 鱼惊荡桨跳。

孤舟宿何许？ 霜月系枫桥。

注：吴松：即吴淞，江名。

小题1:开头两句描写了怎样的景色 ？ 营造了怎样的氛围？（3分）

小题2:请结合全诗分析“孤舟”这一意象的作用。（5分）
查看答案
名词解释

假借
查看答案