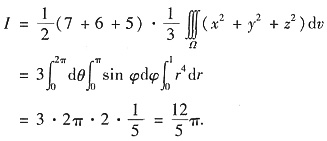问题
填空题
设Ω0=(x,y,z)|x2+y2+z2≤1,z≥0,则
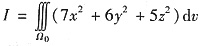 =______.
=______.
答案
参考答案:
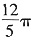
解析:[考点] 计算三重积分
记Ω={(x,y,z)|x2+y2+z2≤1},即Ω0是Ω在xOy面的上半球.
由于f(x,y,z)=7x2+6y2+5z2关于z是偶函数,故
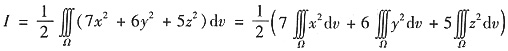
注意到积分区域Ω对x,y,z有轮换对称性,而积分值仅与积分域及被积函数有关,因此
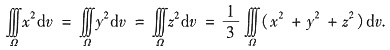
从而
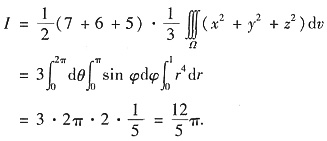
设Ω0=(x,y,z)|x2+y2+z2≤1,z≥0,则
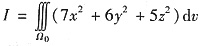 =______.
=______.
参考答案:
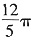
解析:[考点] 计算三重积分
记Ω={(x,y,z)|x2+y2+z2≤1},即Ω0是Ω在xOy面的上半球.
由于f(x,y,z)=7x2+6y2+5z2关于z是偶函数,故
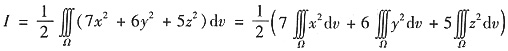
注意到积分区域Ω对x,y,z有轮换对称性,而积分值仅与积分域及被积函数有关,因此
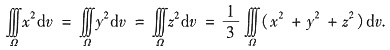
从而