问题
问答题
设f(x，y，z)是连续函数，当t→0+时，[*]是否为无穷小量？如果是，指出它的阶.
答案
参考答案：f(x，y，z)是连续函数，依积分中值定理，存在点(ξ，η，ζ)∈{(x，y，z)|x2+y2+z2≤t2}，使
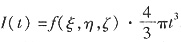. 当t→0+时，(ξ，η，ζ)→(0，0，0).
于是，
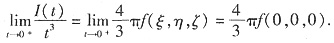
当f(0，0，0)≠0时，Ι(t)是t的3阶无穷小量；当f(0，0，0)=0时，Ι(t)是比t3高阶的无穷小量，从而当t→0+时，Ι(t)至少是t的3阶无穷小量.