问题
问答题
设函数z=(1+ey)cosx-yey. 试证此函数有无穷多个极大值点，而没有极小值点.
答案
参考答案：
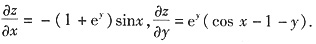
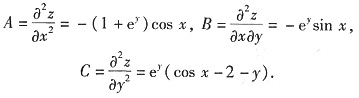
令
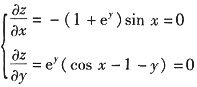，驻点为(x，y)=(2nπ，0)或(x，y)=[(2n+1)π，-2](n=0，±1，±2，…).
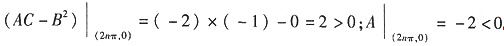. 从而(2nπ，0)(n=0，±1，±2，…)无穷多个点为函数极大值点.
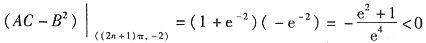，故((2n+1)π，-2)不是函数的极值点，即函数有无穷多个极大值点，而没有极小值点.
解析：[考点] 二元函数极值点