问题
问答题
设抛物线y=ax2+bx+c满足两个条件：
(Ⅰ)过(0，0)和(1，2)两点，且a＜0；
(Ⅱ)与曲线y=-x2+2x围成图形面积最小，
求此抛物线方程.
答案
参考答案：y=ax2+bx+c过(0，0)，(1，2)两点，得
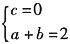，即c=0，b=2-a. y=-x2+2x=-(x-1)2+1，抛物线开口向下，顶点为(1，1)，过(0，0)，(2，0)两点.
设二抛物线另一交点为A，由
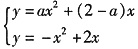得x1=0，
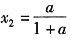，即A点横坐标为
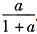. 二曲线所围图形面积为
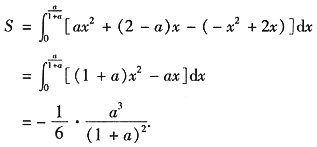
令
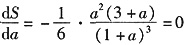，则a=-3∈(-∞，0)为唯一驻点(a=0与a＜0矛盾，舍之).
且
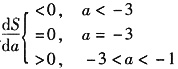，即a=-3为唯一极小点，故为最小点.
此时b=2-(-3)=5. 所求抛物线方程为y=-3x2+5x.
解析：[考点] 定积分应用