问题
问答题
在曲线y=x2（x≥0）上某点A（a，a2）处作切线，使该切线与曲线及x轴所围成的图形的面积为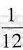
．试求：
（1）切点A的坐标（（a，a2）．
（2）过切点A的切线方程．
答案
参考答案：
由于y=x2，则y’=2x，曲线y=x2上过点A(a，a2)的切线方程为
y-a2=2a(x-a)，
即 y=2ax-a2，
曲线y=x2，其过点A(a，a2)的切线及x轴围成的平面图形的面积
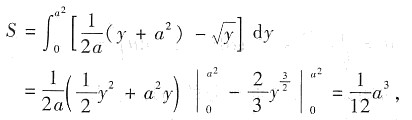
由题设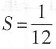
，可得a=1，
因此A点的坐标为(1，1)．
过A点的切线方程为y-1=2(x-1)或y=2x-1．
解析：
本题考查的知识点为定积分的几何意义和曲线的切线方程．
本题在利用定积分表示平面图形时，以y为积分变量，以简化运算，这是值得注意的技巧．