问题
问答题
求y=xex的极值及曲线的凹凸区间与拐点.
答案
参考答案:
y=xex的定义域为(-∞,+∞),
y’=(1+x)ex,
y"=(2+x)ex.
令y’=0,得驻点x1=-1.
令y"=0,得x2=-2.

极小值点为x=-1,极小值为
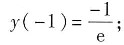
曲线的凹区间为(-2,+∞);
曲线的凸区间为(-∞,-2);
解析:
本题考查的知识点为:描述函数几何性态的综合问题.
求y=xex的极值及曲线的凹凸区间与拐点.
参考答案:
y=xex的定义域为(-∞,+∞),
y’=(1+x)ex,
y"=(2+x)ex.
令y’=0,得驻点x1=-1.
令y"=0,得x2=-2.

极小值点为x=-1,极小值为
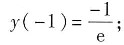
曲线的凹区间为(-2,+∞);
曲线的凸区间为(-∞,-2);
解析:
本题考查的知识点为:描述函数几何性态的综合问题.