问题
问答题
袋中装有5个白球，3个红球，第一次从袋中任取一球，取后不放回，第二次从袋中任取2球，用Xi表示第i次取到的白球数，i=1，2.
(Ⅰ)求(X1，X2)的联合分布；
(Ⅱ)求PX1=0，X2≠0，PX1X2=0；
(Ⅲ)判断X1，X2是否相关，是正相关还是负相关.
答案
参考答案：(Ⅰ)X1的可能取值为0，1；X2的取值为0，1，2. 由乘法公式可得
得联合分布与边缘分布如下
(Ⅱ)P{X1=0，X2≠0}=P{X1=0，X2=1}+P{X1=0，X2=2}=
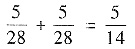
P{X1X2=0}=1-P{X1X2≠0}=1-[P{X1=1，X2=1}+P{X1=1，X2=2}]
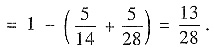
或
P{X1X2=0}=P{X1=0，X2=0}+P{X1=0，X2≠0}+P{X1≠0，X2=0}
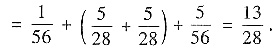
(Ⅲ)由边缘分布知
，而
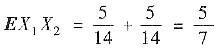
故
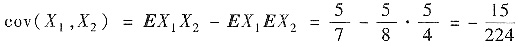
由于协方差不为零且为负数，故知X1，X2负相关.