问题
问答题
设A(2，2)，B(1，1)，，Γ是从点A到点B的线段
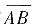下方的一条光滑定向曲线y=y(x)，且它与
围成的面积为2，又φ(y)有连续导数，求曲线积分
答案
参考答案：把该曲线积分分成两部分，其中一个积分的被积表达式易求原函数，另一积分可添加辅助线
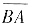后用格林公式.
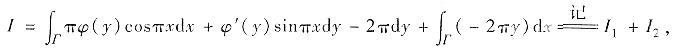
其中
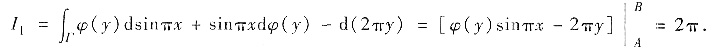
为用格林公式求Ι2，添加辅助线
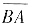. Γ与
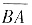围成区域D，并构成D的负向边界，于是
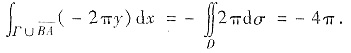
又
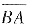的方程：y=x，x∈[1，2]，则
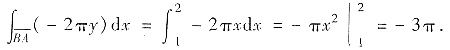
因此
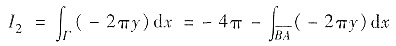
=-4π+3π=-π.
故Ι=Ι1+Ι2=π.
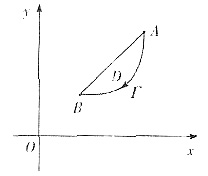
解析：将Ι表成
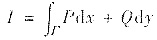，也可添加辅助线
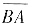，对整个积分Ι在
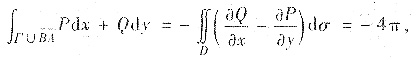与Γ围成的区域D上用格林公式得
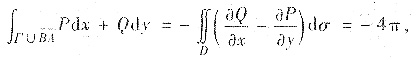
其中
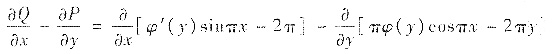
=πφ′(y)cosπx-πφ′(y)cosπx+2π=2π.
又在
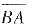上，y=x(x∈[1，2])，
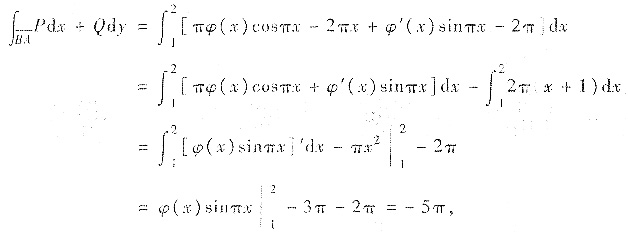
国此，Ι=-4π+5π=π.