设随机变量X的密度函数关于x=μ对称，F(x)为其分布函数，则有
A．F(μ+x)=F(μ-x).
B．F(μ+x)+F(μ-x)＞1.
C．0＜F(μ+x)+F(μ-x)＜1.
D．F(μ+x)+F(μ-x)=1.
参考答案：D
解析：利用分布函数与密度函数的关系及密度函数的对称性，作积分变量替换可导出所需要的结论.
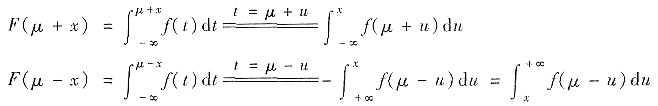
又f(μ-u)=f(μ+u)，u∈(-∞，+∞)
所以
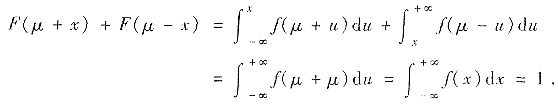
故选D.
作为选择题可以通过特例加以判断，例如X～N(0，1)密度函数关于x=0对称，即逸μ=0，有f(-x)=f(x). 故
F(-x)+F(x)=Φ(x)+Φ(-x)=Φ(x)+1-Φ(x)=1.
但Φ(-x)≠Φ(x)(x≠0). 这样正确选项立即得到了.
本学期我校高中部“阳光志愿者”组织为贫困孩子捐款捐物献爱心活动，同学在积极捐款的同时, 对捐款捐物数额的多少展开了热烈的讨论。请根据表格中提示内容，以 “Does the Amount of Donations Matter Much?”为题，写一篇120字左右的短文, 反映同学们的不同想法。
1．对所给要点不要简单翻译，要有适当发挥； 2．词数：120词左右。 3．参考词汇：爱心－compassion；经济状况—financial condition 4．开头已给出，不计入总词数。 Does the Amount of Donations Matter Much? To help the people in depressed areas in China, students of Senior High Division in Northeast Yucai School were making donations to offer compassion. But__________________ _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ |