问题
问答题
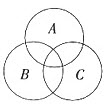
(1)P(A)表示事件A发生的概率，证明P(A∪B)=P(A)+P(B)-P(A∩B)；
(2)若P(A∩B)=P(A)P(B)，则称事件A、B独立；若事件A、B、C两两独立，且P(A∩B∩C)=P(A)P(B)P(C)，则称事件A、B、C独立。设事件A、B、C独立，证明事件A∪B与事件C独立。
答案
参考答案：
证明：(l)由于A∪B=A∪(B-AB)且A∩(B-AB)=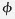
，由概率的可加性，
P(A∪B)=P(A∪(B-AB))=P(A)+P(B-AB)
=P(A)+P(B)-P(AB)
(2)∵事件A、B、C独立
∴P(A∩C)=P(A)P(C)，P(B∩C)=P(B)P(C)，P(A∩B)=P(A)P(B)
且P(A∩B∩C)=P(A)P(B)P(C)
那么，P((A∪B)∩C)=P((A∩C)∪(B∩C))
=P(A∩C)+P(B∩C)-P(A∩B∩C)
=P(A)P(C)+P(B)P(C)-P(A)P(B)P(C)
=P(C)(P(A)+P(B)-P(A)P(B))
=P(C)(P(A)+P(B)-P(A∩B))
=P(C)P(A∪B)
所以，事件A∪B与事件C独立。