参考答案：B

解析：

方法一，设球面方程为x²+y²+z²+2px+2qy+2rz+d=0，则过球面上点(x₀，y₀，z₀)的切平面方程为：

x₀x+y₀y+z₀z+p(x+x₀)+q(y+y₀)+r(z+z₀)+d=0.

由x²+y²+z²-2x+2y-4z-3=0可知，此曲面为球面，且：p=-1，q=1，r=-2，d=-3，又点(3，-2，4)在球面上，则切平面

方程为：2x-y+2z=16，故选B。

方法二：曲面x²+y²+z²-2x+2y-4z-3=0为球面，标准方程为：

(x-1)²+(y+1)²+(z-2)²=9

球心为(1，-1，2)，半径为3。在A、B、C、D四个选项中，只有B、C过点(3，-2，4)。故A、D排除。同时球心到切平面的距离应该等于球的半径，选项B，球心到平面的距离为

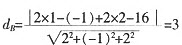
等于球半径，满足题意。故选B。