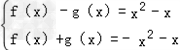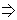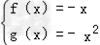问题
解答题
设f（x）是奇函数，g（x）是偶函数，并且f（x）-g（x）=x2-x，求f（x），g（x）
答案
解：f（x）为奇函数，∴f（-x）=-f（x）；
g（x）为偶数，∴g（-x）=g（x）．
f（x）-g（x）=x2-x
∴f（-x）-g（-x）=x2+x
从而-f（x）-g（x）=x2+x，
即f（x）+g（x）=-x2-x，
搜题请搜索小程序“爱下问搜题”
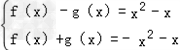
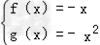
设f（x）是奇函数，g（x）是偶函数，并且f（x）-g（x）=x2-x，求f（x），g（x）
解：f（x）为奇函数，∴f（-x）=-f（x）；
g（x）为偶数，∴g（-x）=g（x）．
f（x）-g（x）=x2-x
∴f（-x）-g（-x）=x2+x
从而-f（x）-g（x）=x2+x，
即f（x）+g（x）=-x2-x，
