问题
填空题
设
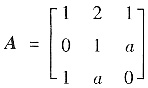 ,B是3阶非零矩阵,满足BA=0,则矩阵B=______.
,B是3阶非零矩阵,满足BA=0,则矩阵B=______.
答案
参考答案:
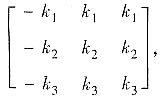 其中k1,k2,k3不全为0.
其中k1,k2,k3不全为0.
由BA=0知r(B)+r(A)≤3. 又由B≠0知r(B)≥1.
显然A中有2阶子式非0,知r(A)≥2. 故必有r(A)=2,r(B)=1.
由
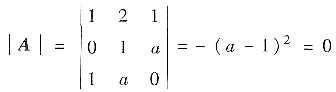 ,得a=1.
,得a=1.
因ATBT=0,所以齐次线性方程组ATx=0的解就是B的行向量,又由
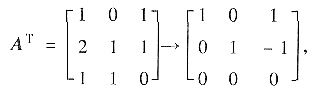
可知ATx=0的通解为k(-1,1,1)T.
故
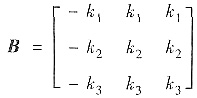 ,其中k1,k2,k3不全为0.
,其中k1,k2,k3不全为0.
AB=0是一个常考的知识点:一方面要意识到矩阵B的列向量是齐次方程组Ax=0的解;另一方面要有秩的信息,即r(A)+r(B)≤n,其中n是A的列向量的个数(当然也是B的行向量的个数).
